Publications
Group highlights
(For a full list see below or go to Google Scholar, ResearcherID)
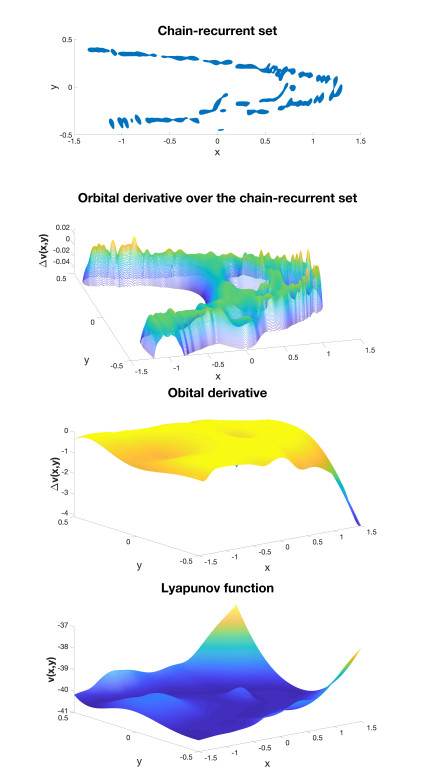
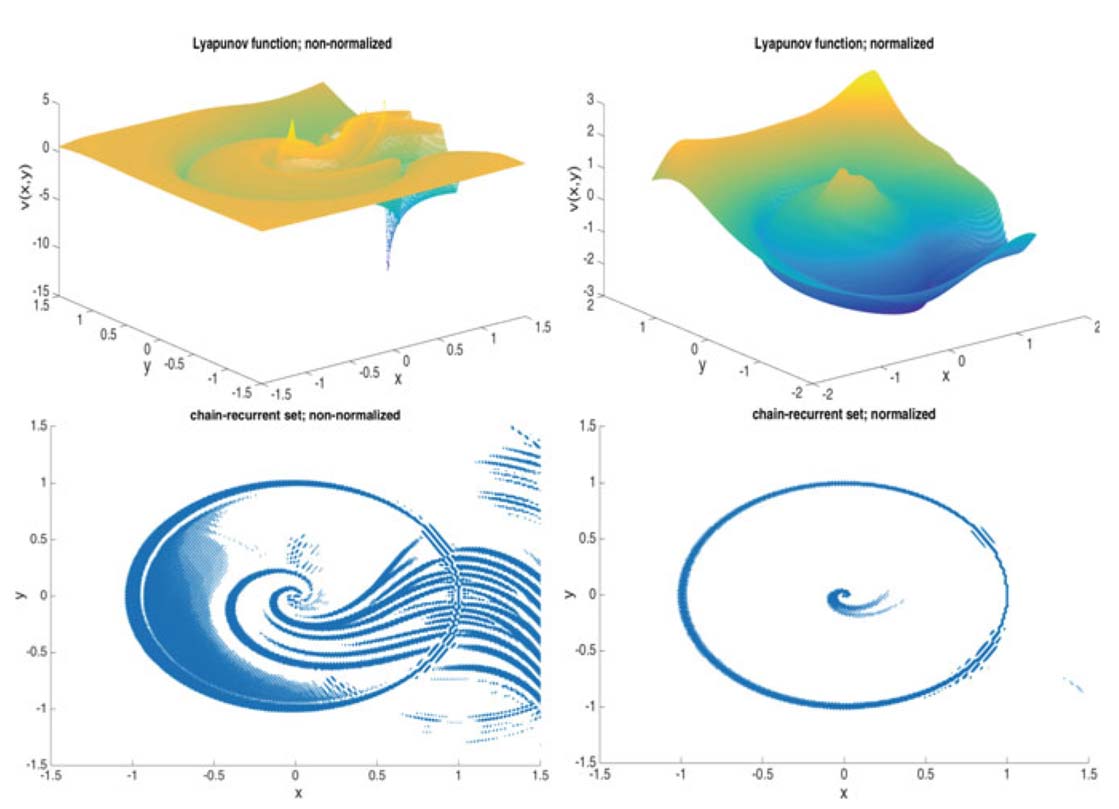
A complete Lyapunov function characterizes the behaviour of a general discrete-time dynamical system. In particular, it divides the state space into the chain-recurrent set where the complete Lyapunov function is constant along trajectories and the part where the flow is gradient-like and the complete Lyapunov function is strictly decreasing along solutions. Moreover, the level sets of a complete Lyapunov function provide information about attractors, repellers, and basins of attraction. We propose two novel classes of methods to compute complete Lyapunov functions for a general discrete-time dynamical system given by an iteration. The first class of methods computes a complete Lyapunov function by approximating the solution of an ill-posed equation for its discrete orbital derivative using meshfree collocation. The second class of methods computes a complete Lyapunov function as solution of a minimization problem in a reproducing kernel Hilbert space. We apply both classes of methods to several examples.
P. Giesl, Z. Langhorne, C. Argáez, S. Hafstein
Discrete and Continuous Dynamical Systems Series B 26, 2021, no. 1, 299–336
Motivated by the desire to compute complete Lyapunov functions for nonlinear dynamical systems, we develop a general theory of discretizing a certain type of con- tinuous minimization problems with differential inequality constraints. The resulting discretized problems are quadratic optimization problems, for which there exist effi- cient solution algorithms, and we show that their unique solutions converge strongly in appropriate Sobolev spaces to the unique solution of the original continuous problem. We develop the theory and present examples of our approach, where we compute complete Lyapunov functions for nonlinear dynamical systems. A complete Lyapunov function characterizes the behaviour of a general dynamical system. In particular, the state space is divided into the chain-recurrent set, where the complete Lyapunov function is constant along solutions, and the part characterizing the gradient-like flow, where the complete Lyapunov function is strictly decreasing along solutions. We propose a new method to compute a complete Lyapunov func- tion as the solution of a quadratic minimization problem, for which no information about the chain-recurrent set is required. The solutions to the discretized problems, which can be solved using quadratic programming, converge to the complete Lyapunov function.
P. Giesl, C. Argáez, S. Hafstein, H. Wendland
Mathematics of Computation, 2021, pp. 1-23
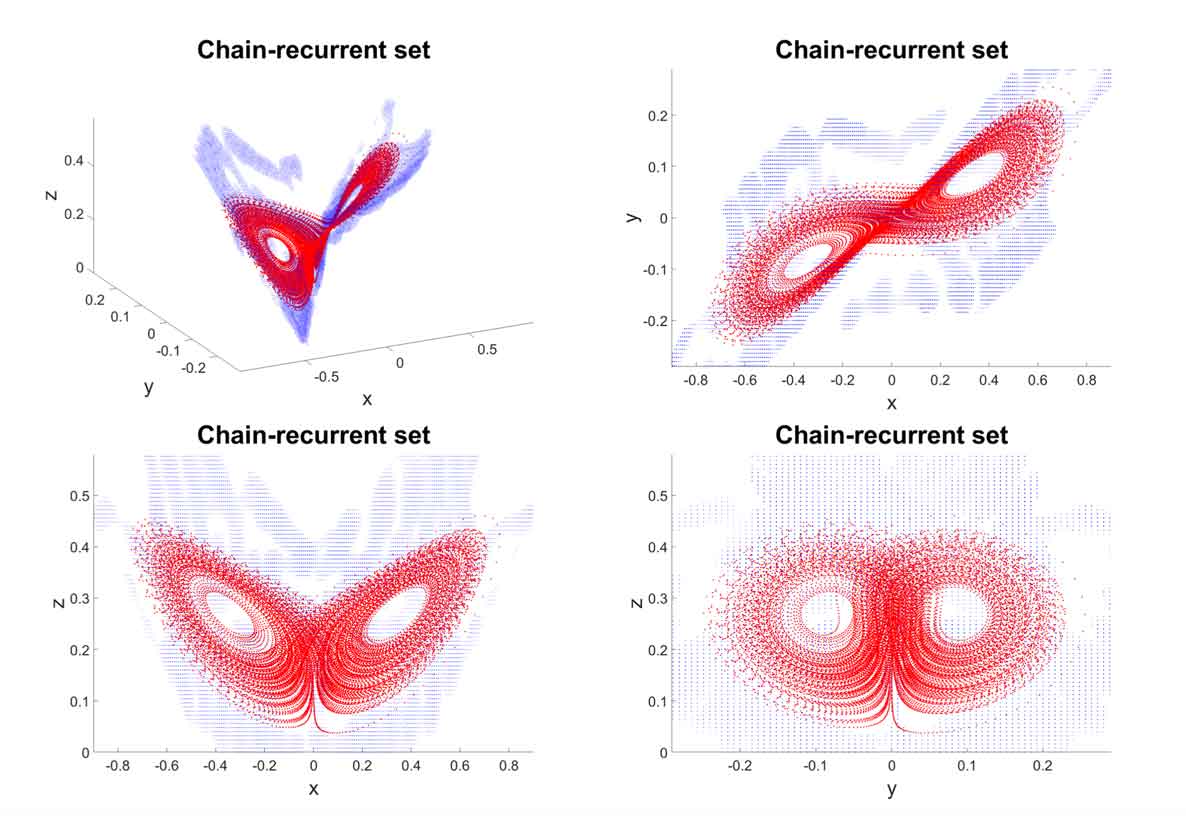
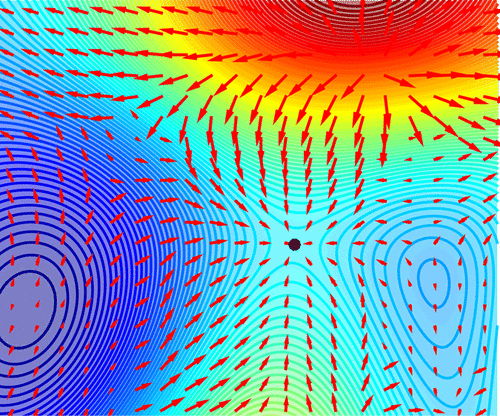
Complete Lyapunov functions (CLF) are scalar-valued functions, which are non-increasing along solutions of a given autonomous ordinary differential equation. They separate the phase-space into the chain-recurrent set, where the CLF is constant along solutions, and the set where the flow is gradient-like and the CLF is strictly decreases along solutions. Moreover, one can deduce the stability of connected components of the chain-recurrent set from the CLF. While the existence of CLFs was shown about 50 years ago, in recent years algorithms to construct CLFs have been designed to determine the chain-recurrent set using the orbital derivative. These algorithms require iterative methods that constructed better and better approximations to a CLF, based on previous iterations. A drawback of these methods is the overestimation of the chain-recurrent set, which has been addressed by different methods. In this paper, we construct a CLF using the previous method, but in contrast to previous work we will use the norm of the gradient of the computed CLF, rather than its orbital derivative, to determine the chain-recurrent set. We will show in this paper that this new approach determines the chain-recurrent set very well without the need of iterations or further methods to reduce the overestimation.
C. Argáez, P. Giesl, S. Hafstein
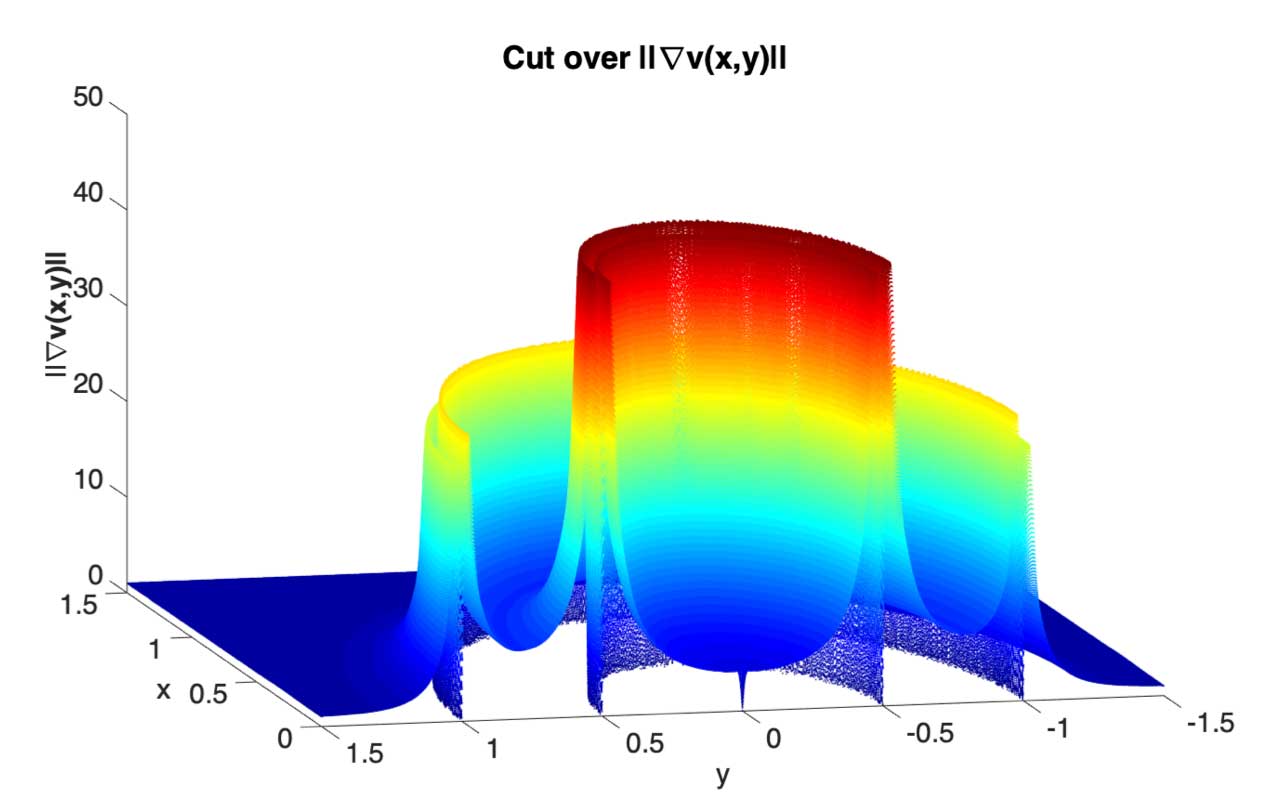
This is an update to PII: S2352711019302109 LyapXool is a C++ program to compute complete Lyapunov functions and their orbital derivatives for any dynamical system expressed by an autonomous ordinary differential equation. Novel features and the improvements made in the second version are discussed. In particular, the gradient of the complete Lyapunov function and its Hessian, together with its eigenvalues and corresponding eigenvectors, are now computed by the software. This information can be used to analyse the attractivity and dimensions of the components of the chain-recurrent set. Further, the structure of the program is now object-oriented rather than procedural. The user friendliness of the program has been improved. This paper describes how the code is organised, how it can be used to compute complete Lyapunov functions and analyse chain-recurrent sets for dynamical systems, and it provides an interesting example of its application.
C. Argáez, P. Giesl, S. Hafstein
SoftwareX, Volume 12, 2020, 100616
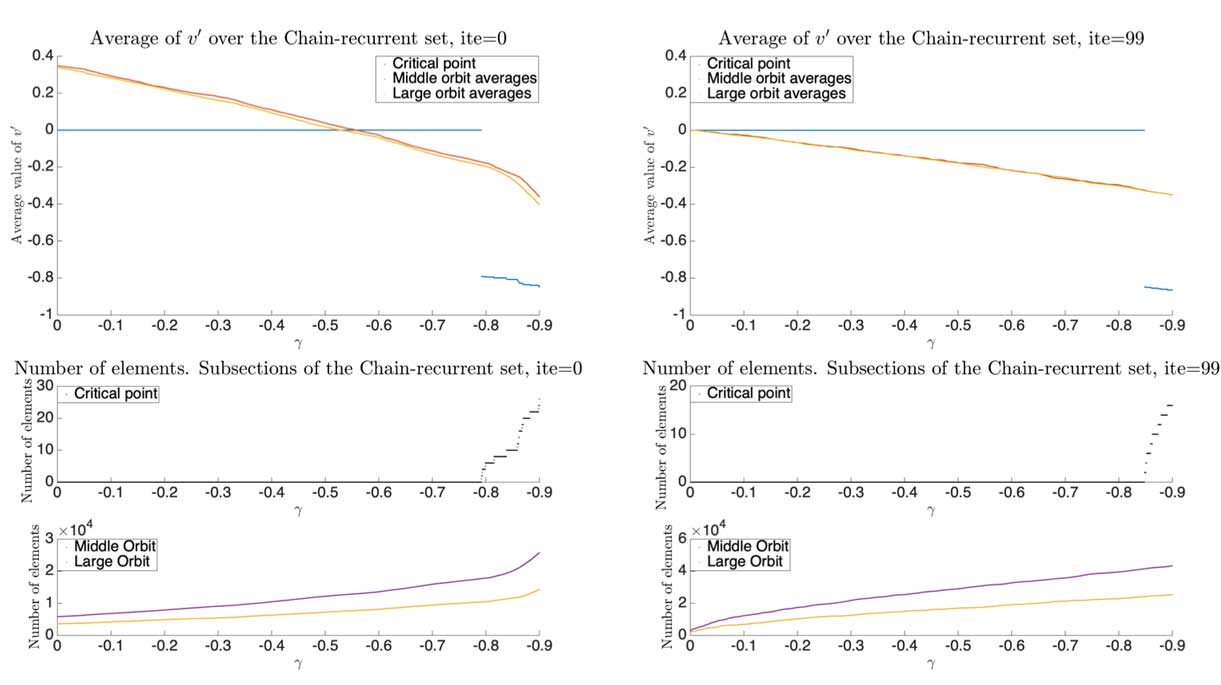
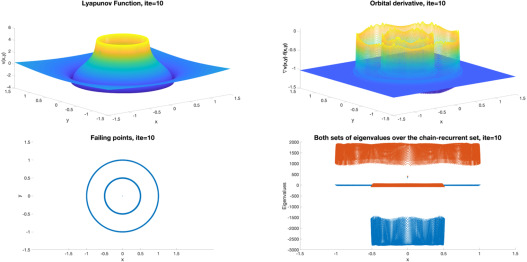
Complete Lyapunov functions for non-linear dynamical systems can be ob- tained by approximately solving a partial differential equation that describes a condi- tion for its orbital derivative. Efficient algorithms to compute them have been imple- mented. The fact that the partial differential equation is not satisfied at points of the chain-recurrent set is used to determine it; more precisely, all points where the value of the orbital derivative is larger than a fixed, critical tolerance parameter, are an estimate of the chain-recurrent set. The mathematical conditions of smoothness of the orbital derivative are obtained by locally averaging the values of the orbital derivative. Further- more, convergence to zero is avoided by normalizing the sum of the orbital derivative condition. However, the tolerance parameter to describe the chain-recurrent set has not been considered. This results in an overestimation of the chain-recurrent set. Several al- gorithms have been proposed to reduce the overestimation of the chain-recurrent set, but no systematic analysis on the dependence on the critical parameter has been made so far. In this paper, we focus on studying this parameter. To proceed, the chain-recurrent set is divided into different subsets of connected components; their evolution per iteration and their different behaviour are studied. The outcome of this research will create an efficient analysis method for locating the chain-recurrent set and aims to reduce its over- estimation by obtaining the tightest possible tolerance parameter necessary to classify it.
C. Argáez, P. Giesl, S. Hafstein
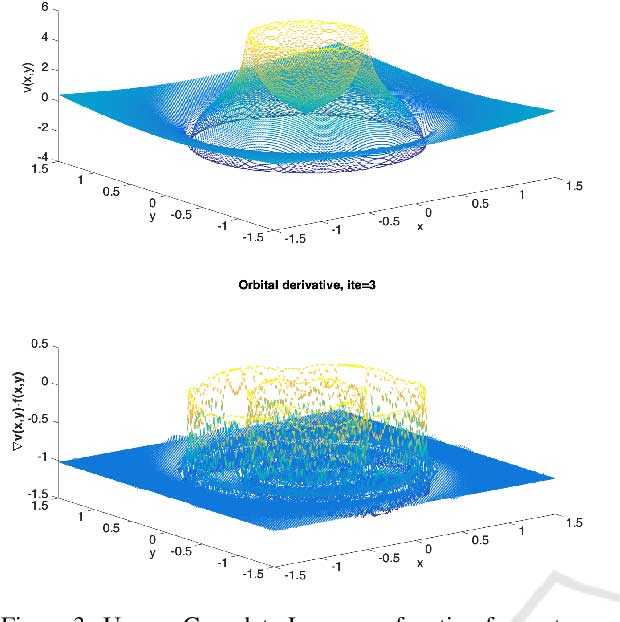
Describing dynamical systems requires capability to isolate periodic behaviour. In Lyapunov’s theory, the qualitative behaviour of a dynamical system given by a differential equation can be described by a scalar function that decreases along solutions: the Complete Lyapunov Function. The chain-recurrent set will pro- duce constant values of an associated complete Lyapunov function and zero values of its orbital derivative. Recently, we have managed to isolate the chain-recurrent set of different dynamical systems in 2- and 3- di- mensions. An overestimation, however, is always obtained. In this paper, we present a method to reduce such overestimation based on geometrical middle points for 2-dimensional systems.
C. Argáez, P. Giesl, S. Hafstein
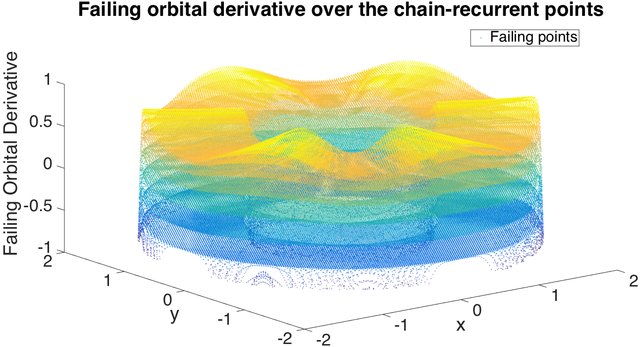
Many advances and algorithms have been proposed to obtain complete Lyapunov functions for dynamicalsystems and to properly describe the chain-recurrent set, e.g. periodic orbits. Recently, a heuristic algorithmwas proposed to classify and reduce the over-estimation of different periodic orbits in the chain-recurrentset, provided they are circular. This was done to investigate the effect on further iterations of the algorithmto compute approximations to a complete Lyapunov function. In this paper, we propose an algorithm thatclassifies the different connected components of the chain-recurrent set for general systems, not restricted to(circular) periodic orbits. The algorithm is based on identifying clustering of points and is independent of theparticular algorithm to construct the complete Lyapunov functions.
C. Argáez, P. Giesl, S. Hafstein
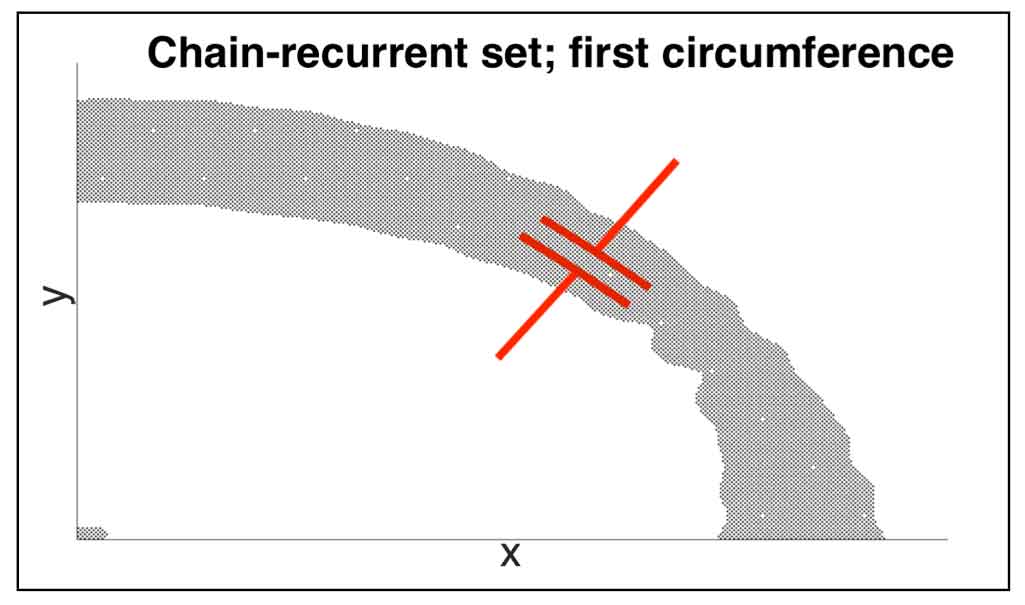
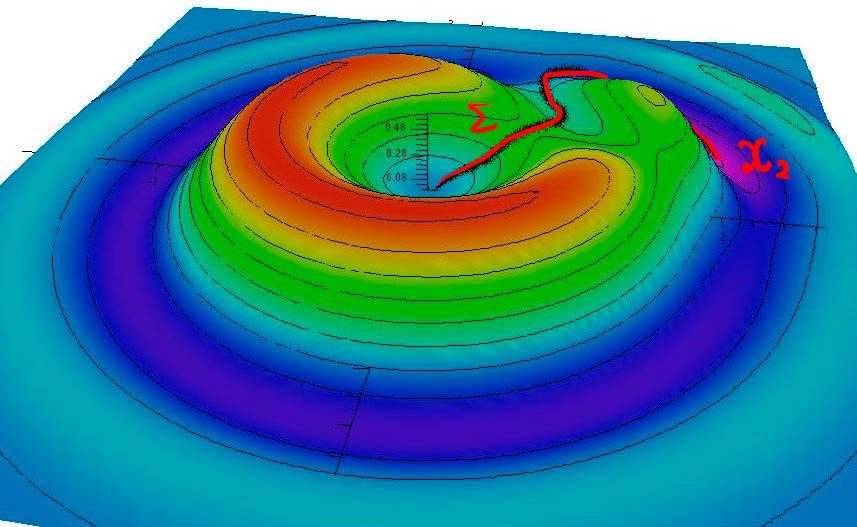
When studying the behaviour of dynamical systems, one particular goal is to find and isolate the periodic solutions and the equilibria. They are a subset of the chain-recurrent set of the dynamical system. In recent work, many improvements have been achieved in computing an approximation of a complete Lyapunov function of a given dynamical system and thus to identify the chain-recurrent set. A weak point in this approach, however, has been an over-estimation of the chain-recurrent set. In this work, we introduce a heuristic algorithm that reduces the overestimation in a simple and efficient way. Furthermore, a new and improved grid to evaluate the complete Lyapunov function is introduced to avoid unevaluated regions in the domain of the function.
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 18th European Control Conference (ECC), Napoli, Italy, 2019, pp. 1622–1627.
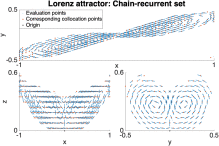
LyapXool is a C++ program to compute complete Lyapunov functions and their orbital derivatives for any two- or three-dimensional dynamical system expressed by an autonomous ordinary differential equation. The program is user-friendly and determines the chain-recurrent set. This paper describes how the code is organized, how it can be used and provides an interesting example of its application.
C. Argáez, J.-C. Berthet, H. Björnsson, P. Giesl, S. F. Hafstein
SoftwareX, Volume 10, July–December 2019, 100325
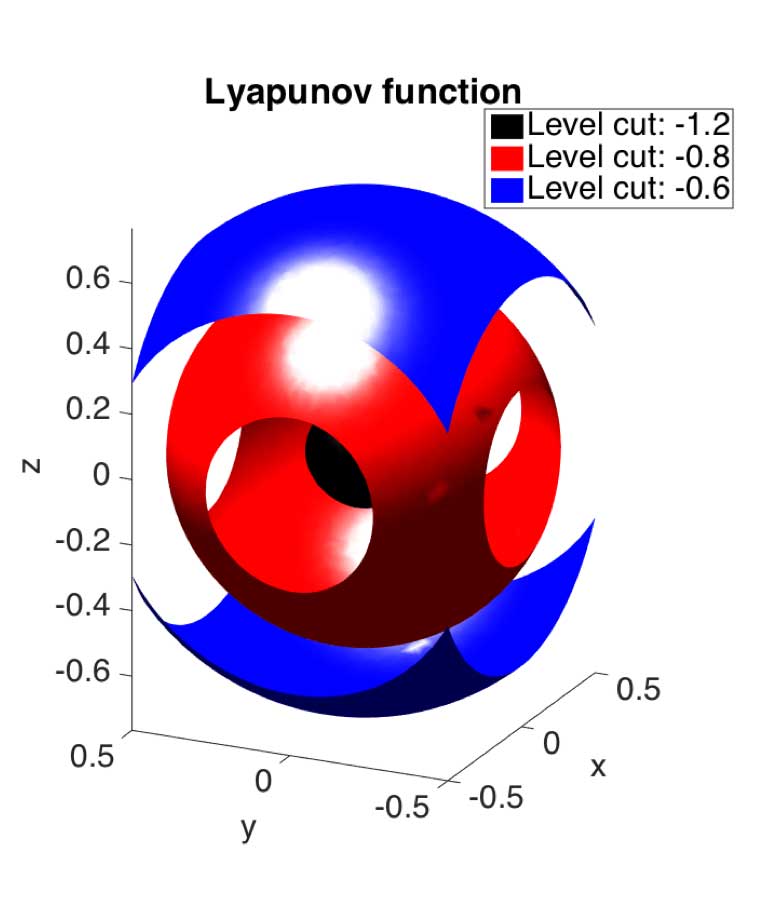
Complete Lyapunov functions are of much interestin control theory because of their capability to describe the long-time behaviour of nonlinear dynamical systems. The state-spaceof a system can be divided in two different regions determinedby a complete Lyapunov function: the region of the gradient-like flow, where the Lyapunov function is strictly decreasingalong solution trajectories, and the chain-recurrent set whosechain-transitive components are level sets of the Lyapunovfunction. There has been continuous effort to properly identifyboth regions and in this paper we discuss the extension of ourmethods to compute complete Lyapunov functions in the planeto the three-dimensional case, which is directly applicable tohigher dimensions, too. When extending the methods to higherdimensions, the number of points for collocation and evaluationgrows exponentially. To keep the number of evaluation pointsunder control, we propose a new way to choose them, whichdoes not depend on the dimension.
C. Argáez, P. Giesl, S. Hafstein
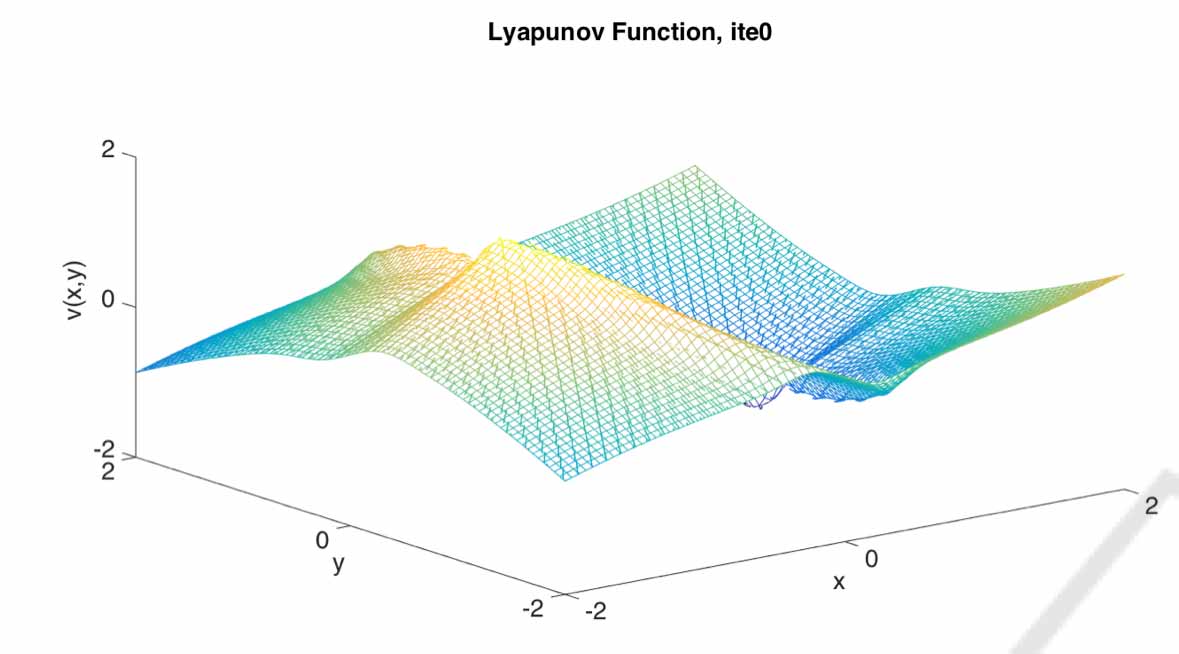
Differential equations describe many interesting phenomena arising from various disciplines. This includes many important models, e.g. predator-prey in population biology or the Van der Pol oscillator in electrical engineering. Complete Lyapunov functions allow for the sys- tematic study of the qualitative behaviour of complicated systems. In this paper, we extend the analysis of the algorithm presented in [1]. We study the efficiency of our algorithm and discuss important sections of the code.
C. Argáez, P. Giesl, S. Hafstein
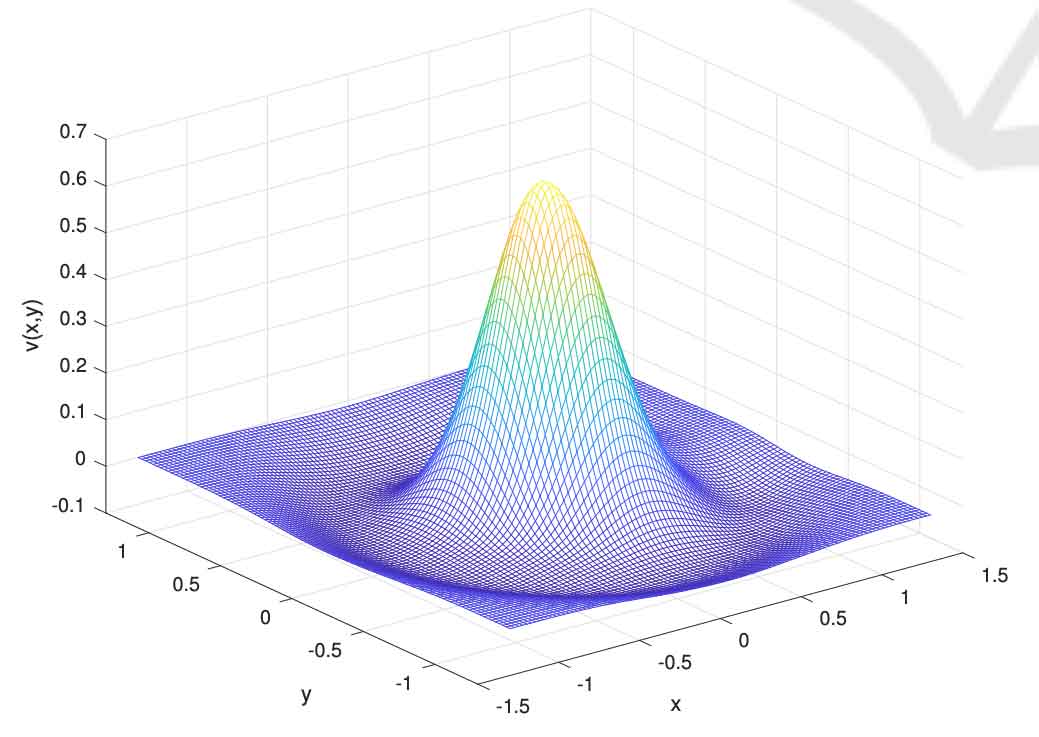
A complete Lyapunov function characterizes the behaviour of a general dynamical system. In particular, the state space is split into the chain-recurrent set, where the function is constant, and the part characterizing the gradient-like flow, where the function is strictly decreasing along solutions. Moreover, the level sets of a complete Lyapunov function provide information about the stability of connected components of the chainrecurrent set and the basin of attraction of attractors therein. In a previous method, a complete Lyapunov function was constructed by approximating the solution of the PDE V’(x) = −1, where the prime denotes the orbital derivative, by meshfree collocation. We propose a new method to compute a complete Lyapunov function: we only fix the orbital derivative V’(x0) = −1 at one point, impose the constraints V’(x) ≤ 0 for all other collocation points and minimize the corresponding reproducing kernel Hilbert space norm. We show that the problem has a unique solution which can be computed as the solution of a quadratic programming problem. The new method is applied to examples which show an improvement compared to previous methods.
C. Argáez, P. Giesl, S. Hafstein
The minimum mode following method for finding first order saddle points on an energy surface is used, for example, in simulations of long time scale evolution of materials and surfaces of solids. Such simulations are increasingly being carried out in combination with computationally demanding electronic structure calculations of atomic interactions, so it is essential to reduce as much as possible the number of function evaluations needed to find the relevant saddle points. Several improvements to the method are presented here and tested on a benchmark system involving rearrangements of a heptamer island on a close packed crystal surface. Instead of using a uniform or Gaussian random initial displacement of the atoms, as has typically been done previously, the starting points are arranged evenly on the surface of a hypersphere and its radius is adjusted during the sampling of the saddle points. This increases the diversity of saddle points found and reduces the chances of reconverging on previously located saddle points. The minimum mode is estimated using the Davidson method, and it is shown that significant savings in the number of function evaluations can be obtained by assuming the minimum mode is unchanged until the atomic displacement exceeds a threshold value. The number of function evaluations needed for a recently published benchmark (S. T. Chill et al. J. Chem. Theory Comput. 2014, 10, 5476) is reduced to less than a third with the improved method as compared with the best previously reported results.
C. Argaez, M. Melgaard
J. Chem. Theory Comput., 2017, 13 (1), pp 125-134
Ordinary differential equations arise in a variety of applications, including climate modeling, electronics, predator-prey modeling, etc., and they can exhibit highly complicated dynamical behaviour. Complete Lyapunov functions capture this behaviour by dividing the phase space into two disjoint sets: the chain-recurrent part and the transient part. If a complete Lyapunov function is known for a dynamical system the qualitative behaviour of the system’s solutions is transparent to a large degree. The computation of a complete Lyapunov function for a given system is, however, a very hard task. We present significant improvements of an algorithm recently suggested by the authors to compute complete Lyapunov functions. Previously this methodology was incapable to fully detect chain-recurrent sets in dynamical systems with high differences in speed. In the new approach we replace the system under consideration with another one having the same solution trajectories but such that they are traversed at a more uniform speed. The qualitative properties of the new system such as attractors and repellers are the same as for the original one. This approach gives a better approximation to the chain-recurrent set of the system under study.
C. Argáez, P. Giesl, S. Hafstein

Within the Hartree–Fock theory of atoms and molecules, we prove existence of a ground state in the presence of an external magnetic field when: (1) the diamagnetic effect is taken into account; (2) both the diamagnetic effect and the Zeeman effect are taken into account. For both cases, the ground state exists provided the total charge (Formula presented.) of the nuclei K exceeds (Formula presented.), where N is the number of electrons. For the first case, the Schrödinger case, we complement prior results by allowing a wide class of magnetic potentials. In the second case, the Pauli case, we include the magnetic field energy in order to obtain a stable problem and we assume (Formula presented.), where (Formula presented.) is the fine structure constant.
C. Argaez, M. Melgaard
Applicable Analysis, pp 1-27, 2017

We study the open-shell, spin-polarized Kohn–Sham models for non-relativistic and quasi-relativistic N-electron Coulomb systems; that is, systems where the kinetic energy of the electrons is given by the quasi-relativistic operator $-\Delta_{x_n}$ or the quasi-relativistic operator $\sqrt{-\alpha^{-2}\Delta_{x_n}+\alpha^{-4}}-\alpha^{-2}$. For standard and extended Kohn–Sham models in the local density approximation, we prove existence of a ground state (or minimizer) provided that the total charge Ztot of K nuclei is greater than N-1. For the quasi-relativistic setting we also need that is smaller than a critical charge Z_c=2\alpha^{-1}\pi^{-1}.
C. Argaez, M. Melgaard
Methods and Applications of Analysis, Vol. 23, No. 2, pp. 269-292, 2016.

We study the standard and extended Kohn-Sham models for quasi- relativistic N-electron Coulomb systems; that is, systems where the kinetic energy of the electrons is given by the quasi-relativistic operator $\sqrt{-\alpha^{-2}\Delta_{x_n}+\alpha^{-4}}-\alpha^{-2}$. For spin-unpolarized systems in the local density approximation, we prove existence of a ground state (or minimizer) provided that the total charge Ztot of K nuclei is greater than N − 1 and that Ztot is smaller than a critical charge Z_c=2\alpha^{-1}\pi^{-1}.
C. Argaez, M. Melgaard
Electronic Journal of Differential Equations, Vol. 2012 (2012), No. 18, pp. 1–20.
We establish existence of infinitely many distinct solutions to the multi-configurative Hartree-Fock type equations for N-electron Coulomb systems with quasi-relativistic kinetic energy for the n th electron. Finitely many of the solutions are interpreted as excited states of the molecule. Moreover, we prove existence of a ground state. The results are valid under the hypotheses that the total charge Z of K nuclei is greater than N-1 and that Z is smaller than a critical charge. The proofs are based on a new application of the Lions-Fang-Ghoussoub critical point approach to nonminimal solutions on a complete analytic Hilbert-Riemann manifold.
C. Argaez, M. Melgaard
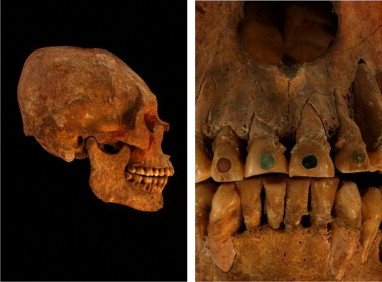
In the island of Jaina, Campeche, red and yellow pigmented bones have been found. The study of the yellow and red colors in these burials is important for their possible interpretation, either religious, intentional coloring, or to understand taphonomic processes such as reactions of the original pigments with other compounds. Yellow color on bones is unusual in prehispanic burials. In this work, the red bones are shown to be pigmented with cinnabar as mentioned for tombs of important Mayan rulers. The yellow pigment is mainly constituted by Fe as shown by X-ray fluorescence. It was identified to be goethite (iron hydroxide) by electron diffraction. By scanning electron microscopy, the thickness of the pigment layer was measured to be ca. 5 microns. Note that hematite iron oxide is red and that it turns out to be yellow with hydroxylation. Hence, it seems that the nowadays yellow bones were originally red; indeed, yellow goethite may be the result of red hematite hydroxylation.
E. Batta, C. Argáez, J. Mansilla, C. Pijoan, P. Bosch
Journal of Archaeological Science, 40, pp. 712-722 (2013)
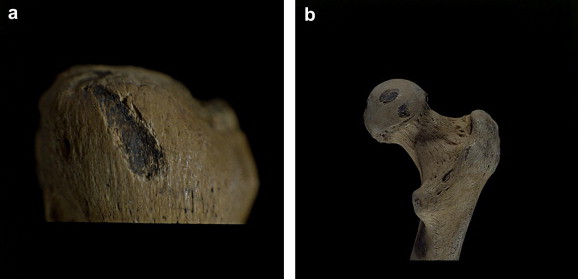
In the island of Jaina, Campeche, red and yellow pigmented bones have been found. The study of the yellow and red colors in these burials is important for their possible interpretation, either religious, intentional coloring, or to understand taphonomic processes such as reactions of the original pigments with other compounds. Yellow color on bones is unusual in prehispanic burials. In this work, the red bones are shown to be pigmented with cinnabar as mentioned for tombs of important Mayan rulers. The yellow pigment is mainly constituted by Fe as shown by X-ray fluorescence. It was identified to be goethite (iron hydroxide) by electron diffraction. By scanning electron microscopy, the thickness of the pigment layer was measured to be ca. 5 microns. Note that hematite iron oxide is red and that it turns out to be yellow with hydroxylation. Hence, it seems that the nowadays yellow bones were originally red; indeed, yellow goethite may be the result of red hematite hydroxylation.
C. Argáez, E. Batta, J. Mansilla, C. Pijoan, P. Bosch
Journal of Archaeological Science, 38, pp. 2979-2988(2011)
Full List
Computing complete lyapunov functions for discrete-time dynamical systems
P. Giesl, Z. Langhorne, C. Argáez, S. Hafstein
Discrete and Continuous Dynamical Systems Series B 26, 2021, no. 1, 299–336
Minimization with differential inequality constraints applied to complete Lyapunov functions
P. Giesl, C. Argáez, S. Hafstein, H. Wendland
Mathematics of Computation, 2021, pp. 1-23
Complete Lyapunov Functions: Determination of the Chain-recurrent set using the Gradient
C. Argáez, P. Giesl, S. Hafstein
Simulation and Modeling Methodologies, Technologies and Applications Series: Advances in Intelligent Systems and Computing 1260 eds. M. Obaidat, T. Ören, and F. De Rango, Springer 2021. pp. 104–12.
Iterative Construction of Complete Lyapunov Functions: Analysis of Algorithm Efficiency.
C. Argáez, P. Giesl, S. Hafstein
Advances in Intelligent Systems and Computing 947,M. Obaidat, T. Ören, and F. De Rango, Springer 2020. pp. 83-100.
Update (22.0) to LyapXool: Eigenpairs and new classification methods, SoftwareX
C. Argáez, P. Giesl, S. Hafstein
SoftwareX, Volume 12, 2020, 100616
Evaluation of Lyapunov Function Candidates Through Averaging Iterations
C. Argáez, P. Giesl, S. F. Hafstein
Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO), 2020, pp. 734–744.
Critical tolerance evolution: Classification of the chain-recurrent set
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 15th International Conference on Dynamical Systems: Theory and Applications (DSTA), Volume: Mathematical and Numerical Aspects of Dynamical System Analysis, Lodz, Poland, 2019, pp. 21–32.
Middle Point Reduction of the Chain-recurrent
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH), Prague, Czech Republic, 2019, pp. 141–152.
Clustering Algorithm for Generalized Recurrences using Complete Lyapunov Functions
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Prague, Czech Republic, 2019, pp. 138–146.
Improved estimation of the chain-recurrent set
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 18th European Control Conference (ECC), Napoli, Italy, 2019, pp. 1622–1627.
LyapXool - a program to compute complete Lyapunov functions
C. Argáez, J.-C. Berthet, H. Björnsson, P. Giesl, S. F. Hafstein
SoftwareX, Volume 10, July–December 2019, 100325
Computation of Complete Lyapunov Functions for Three-Dimensional Systems
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 57rd IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 2018, pp. 4059–4064.
Iterative Construction of Complete Lyapunov Functions
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH), Porto, Portugal, 2018, pp. 211–222.
Construction of a Complete Lyapunov Function using Quadratic Programming
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Porto, Portugal, 2018, pp. 560–568.
A C++ Code to Compute Them
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH), Madrid, Spain, 2017, pp. 323–330.
Analysing Dynamical Systems: Towards Computing Complete Lyapunov Functions
C. Argáez, P. Giesl, S. Hafstein
Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH), Madrid, Spain, 2017, pp. 134–144.
Improved Minimum Mode Following Method for Finding First Order Saddle Points
C. Argaez, M. Melgaard
J. Chem. Theory Comput., 2017, 13 (1), pp 125-134
Computational approach for complete Lyapunov functions
C. Argáez, P. Giesl, S. Hafstein
Dynamical Systems in Theoretical Perspective. Series: Springer Proceedings in Mathematics and Statistics 248 ed. J. Awrejcewicz, Springer 2018. pp. 1–11.
Ground state solutions to Hartree-Fock equations with magnetic fields
C. Argaez, M. Melgaard
Applicable Analysis, pp 1-27, 2017
Minimizers for open-shell, spin-polarised Kohn-Sham equations for non-relativistic and quasi-relativistic molecular systems
C. Argaez, M. Melgaard
Methods and Applications of Analysis, Vol. 23, No. 2, pp. 269-292, 2016.
Existence of a minimizer for the quasi-relativistic Kohn-Sham model
C. Argaez, M. Melgaard
Electronic Journal of Differential Equations, Vol. 2012 (2012), No. 18, pp. 1–20.
Solutions to quasi-relativistic multi-configurative Hartree-Fock equations in quantum chemistry
E. Batta, C. Argáez, J. Mansilla, C. Pijoan, P. Bosch
Nonlinear Analysis: Theory, Methods & Applications, 75 (2012), pp. 384-404. Addendum and erratum, Nonlin. Anal. TMA
On yellow and red pigmented bones found in Mayan burials of Jaina
E. Batta, C. Argáez, J. Mansilla, C. Pijoan, P. Bosch
Journal of Archaeological Science, 40, pp. 712-722 (2013)
The origin of black pigmentation in a sample of Mexican prehispanic human bones
C. Argáez, E. Batta, J. Mansilla, C. Pijoan, P. Bosch
Journal of Archaeological Science, 38, pp. 2979-2988(2011)